Final Answer:
The least residues ( r ) modulo 7 that satisfy
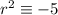 are
are

Step-by-step explanation:
To find the least residues ( r ) modulo 7 satisfying
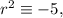 we inspect the quadratic residues for each residue class modulo 7. Squaring each residue class from 0 to 6 and taking the remainders modulo 7, we look for residues that are congruent to -5 (mod 7).
we inspect the quadratic residues for each residue class modulo 7. Squaring each residue class from 0 to 6 and taking the remainders modulo 7, we look for residues that are congruent to -5 (mod 7).
![\[0^2 \equiv 0, \quad 1^2 \equiv 1, \quad 2^2 \equiv 4, \quad 3^2 \equiv 2, \quad 4^2 \equiv 2, \quad 5^2 \equiv 4, \quad 6^2 \equiv 1 \pmod{7}\]](https://img.qammunity.org/2024/formulas/mathematics/college/fonxn3ek8n56l2edt41q6t67d2u8yxhhwm.png)
By inspection, we find that
 and
and
 are the residues satisfying
are the residues satisfying
 Therefore,
Therefore,
 are the least residues modulo 7 that satisfy the given congruence.
are the least residues modulo 7 that satisfy the given congruence.
This result aligns with the concept of quadratic residues and congruences modulo a prime. The solutions are found by examining the squares of residues and identifying those equivalent to -5 modulo 7. The least residues are chosen to ensure we obtain the smallest positive integers that satisfy the congruence.