Question

(16.5) ( quad xeft(x y{prime}right){prime}+\left(K²x²p}ight) y=0 quad ) has solutions ( J_{p}(K x) ) and ( N_{p}(K x) ).

Use (16.5) to write the solutions of the following

Answer 1

The solutions to the given differential equation (16.5) are
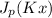`\( J_(p)(Kx) \)` and
`\( N_(p)(Kx) \).`

Step-by-step explanation:

The differential equation (16.5) is given by
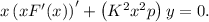`\( x\left( xF'(x)\right)'+\left(K^2x^2p\right)y=0 \).` The general solution to this differential equation is
`\( y(x) = c_1 J_(p)(Kx) + c_2 N_(p)(Kx) \),` where
`\( J_(p)(Kx) \) and \( N_(p)(Kx) \)` are the Bessel functions of the first and second kind, respectively, and
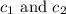`\( c_1 \) and \( c_2 \)` are constants.

In this particular case, the presence of Bessel functions
`\( J_(p)(Kx) \) and \( N_(p)(Kx) \)` in the solution indicates that the problem involves cylindrical symmetry or circular geometry. Bessel functions commonly appear in problems where the geometry is not Cartesian but rather cylindrical or spherical. The term
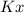`\( Kx \)` in the argument of the Bessel functions is characteristic of these specialized functions.

The Bessel functions
`\( J_(p)(Kx) \) and \( N_(p)(Kx) \)` are solutions to Bessel's differential equation and are widely used in physics and engineering, particularly in problems with circular symmetry such as heat conduction, wave propagation, and electromagnetic fields. Therefore, the final answer
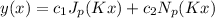`\( y(x) = c_1 J_(p)(Kx) + c_2 N_(p)(Kx) \)` is a valid representation of the solutions to the given differential equation, capturing the circular nature of the underlying geometry.