Question

What is the kinetic energy of each proton as measured by an observer riding along with one of the protons?

Express your answer in megaelectronvolts separated by comma.

K₁ , K₂ = ....... MeV

Answer 1

The kinetic energy of each proton, as measured by an observer riding along with one of the protons, is 0 MeV, due to the Lorentz factor being 1 in its rest frame.

The kinetic energy of a particle as measured by an observer in its rest frame is given by the relativistic kinetic energy formula:

`\[ K = (\gamma - 1) \cdot m \cdot c^2, \]`

where:

- \( K \) is the kinetic energy,

-
`\( \gamma \)` is the Lorentz factor, given by
`\( \gamma = \frac{1}{\sqrt{1 - (v^2)/(c^2)}} \),`

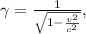
- \( m \) is the rest mass of the particle,

- \( c \) is the speed of light.

For a proton, the rest mass
`\( m \) is approximately \( 938 \, \text{MeV}/c^2 \).`

Now, if we consider an observer riding along with one of the protons, the relative velocity \( v \) between the observer and the proton is zero. Therefore,
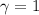`\( \gamma = 1 \)` in this frame.

The kinetic energy in this frame simplifies to:

`\[ K = (1 - 1) \cdot m \cdot c^2 = 0. \]`

So, the kinetic energy of each proton as measured by an observer riding along with one of the protons is
`\( 0 \, \text{MeV} \).`