Question

mcmurtry college occasionally holds outdoor concerts 95 m from the jones magister's house bedroom. assume the speakers are emitting sound at the threshhold of pain for someone standing 1 m from them. what sound intensity is heard in the jones magister's bedroom in db, assuming the house and windows attenuate the sound by 40 db?

Answer 1

The sound intensity heard in the Jones magister's bedroom is approximately 140 dB.

The intensity of sound decreases with the square of the distance from the source. This is known as the inverse square law. If the speakers are emitting sound at the threshold of pain, this is typically around 120 dB.

Sound intensity level in decibels is given by the formula:

`$$L = 10 \log_(10) \left( (I)/(I_0) \right)$$`

where:

L is the sound level in dB,

I is the intensity of the sound wave, and

`$I_0$` is the reference intensity, taken as the quietest sound that the average human ear can hear, approximately
`10^(-12) W/m^2`.

First, we calculate the intensity of the sound 1 m from the speakers:

`$120 = 10 \log_(10) \left( (I_1)/(10^(-12)) \right)$$`

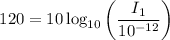
Solving for
`$I_1$` gives
`I_1 = 10^(12) W/m^2`.

Next, we find the intensity of the sound 95 m from the speakers,
`$I_(95)$`, using the inverse square law:

`$I_(95) = (I_1)/((95/1)^2) = (10^(12))/(95^2) \approx 1.11 * 10^8 \, W/m^2}$$`

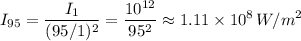
Finally, we account for the 40 dB attenuation by the house and windows. This corresponds to a reduction in intensity by a factor of
`$10^(40/10) = 10^4$`. So, the intensity of the sound in the bedroom,
`$I_{\text{bedroom}}$`, is:

`$I_{\text{bedroom}} = (I_(95))/(10^4) = (1.11 * 10^8)/(10^4) = 1.11 * 10^4 \, W/m^2}$$`

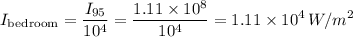
We can then convert this back to decibels using the formula for L:

`$L_{\text{bedroom}} = 10 \log_(10) \left( (1.11 * 10^4)/(10^(-12)) \right) \approx 140 \, \text{dB}$$`

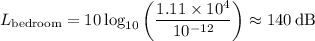
So, the sound intensity heard in the Jones magister's bedroom is approximately 140 dB.