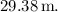the height of the oil layer should be approximately
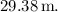
To find the height of the oil layer, we can use the hydrostatic pressure formula. The gauge pressure
 at the bottom of the tank is related to the density
at the bottom of the tank is related to the density
 , gravitational acceleration (\(g\)), and the height (\(h\)) by the equation:
, gravitational acceleration (\(g\)), and the height (\(h\)) by the equation:
![\[ P_{\text{gauge}} = \rho \cdot g \cdot h \]We can rearrange this equation to solve for the height (\(h\)):\[ h = \frac{P_{\text{gauge}}}{\rho \cdot g} \]](https://img.qammunity.org/2024/formulas/physics/high-school/vu0p2zp7brbhwh7u6xk59xg78mvf5l1f3f.png)
Given that the gauge pressure
 is
is
 , the density of the oil
, the density of the oil
 is
is
 , and the density of water
, and the density of water
 is
is
 , and the acceleration due to gravity (\(g\)) is approximately
, and the acceleration due to gravity (\(g\)) is approximately
 , we can substitute these values into the equation:
, we can substitute these values into the equation:
![\[ h = \frac{9.5 * 10^4 \, \text{Pa}}{(670 \, \text{kg/m}^3 - 1000 \, \text{kg/m}^3) \cdot 9.8 \, \text{m/s}^2} \]](https://img.qammunity.org/2024/formulas/physics/high-school/so7llo76vwh4a7rhktye4g8owz0nhlxmpb.png)
First, calculate the difference in densities:
![\[ \Delta \rho = \rho_{\text{water}} - \rho_{\text{oil}} = 1000 \, \text{kg/m}^3 - 670 \, \text{kg/m}^3 \]](https://img.qammunity.org/2024/formulas/physics/high-school/ussu4j6dt8d6332822h3jujc5kb5wdi0r2.png)
Now, substitute into the equation:
 ]
]
Calculate:
![\[ h = \frac{9.5 * 10^4 \, \text{Pa}}{(330 \, \text{kg/m}^3) \cdot 9.8 \, \text{m/s}^2} \]\[ h \approx (9.5 * 10^4)/(3234) \, \text{m} \]\[ h \approx 29.38 \, \text{m} \]](https://img.qammunity.org/2024/formulas/physics/high-school/93ttudh9a5koqp829gujwsxul00fvjtktg.png)
Therefore, the height of the oil layer should be approximately