Question

A random survey of 83 women who were victims of violence found that were attacked by relatives. a random survey of men found that were attacked by relatives. at , can it be shown that the percentage of women who were attacked by relatives is less than the percentage of men who were attacked by relatives?

O use for the proportion of women who were attacked by relatives.
O use the critical value method with tables and round all intermediate calculations to at least three decimal places.

Answer 1

The z-score is less than the critical value, then it means that we will reject the null hypothesis.

How to find the Hypotheses Conclusion?

For sample 1, we have that the sample size is:

N₁ = 83

Number of cases: X₁ = 24

Thus:

Sample proportion: p^₁ = 24/83 = 0.2892

For sample 2, we have that the sample size is:

N₂ = 42

Number of cases: X₂ = 19

Thus:

Sample proportion: p^₂ = 19/42 = 0.4524

The pooled proportion is calculated from the formula:

(X₁ + X₂ )/(N₁ + N₂) = (24 + 19)/(83 + 42)

= 0.344

Since the significance level is α = 0.05, then:

1) Let us define the Hypotheses:

Null hypothesis: H₀: p₁ = p₂

Alternative Hypothesis: Hₐ: p₁ < p₂

This corresponds to a left tailed test for which a z-test for two population proportion needs to be concluded.

2) Rejection Region:

The critical value for a left tailed z-test with a significance level of α = 0.05 is
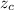`z_(c)` = 1.64

Thus, the rejection region is:

R = {z: z < -1.64}

3) Test Statistic:

The z-score is gotten from the formula:

z =
`\frac{p_(1) - p_(2)}{\sqrt{ p(1 - p)((1)/(n_(1) ) + (1)/(n_(2) ))}}`

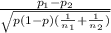
Plugging in the relevant values gives:

z =
`\frac{0.2892 - 0.4524}{\sqrt{ 0.344(1 - 0.344)((1)/(83 ) + (1)/(42))}}`

z = -1.815

4) Decision about the Null Hypothesis:

Since the z-score is less than the critical value, then it means that we will reject the null hypothesis.

Complete question is:

A random survey of 83 women who were victims of violence found that 24 were attacked by relatives. A random survey of 42 men found that 19 were attacked by relatives. At alpha =0.05 , can it be shown that the percentage of women who were attacked by relatives is less than the percentage of men who were attacked by relatives? Use P_1 for the proportion of women who were attacked by relatives. Use the P -value method . (a) State the hypotheses and identify the claim with the correct hypothesis. H_0 : p_1=p_2 not claim H_1 : p_1 claim This hypothesis test is a one-tailed test.

b) Find the P -value. Round your answer to at least four decimal places. P-value =