Question

​​​​​​​

5. Let \( M \subset \mathbb{R}^{3} \) be the paraboloid defined by \( z=x^{2}+y^{2} \). Show that the vector field \( X= \) \( x \frac{\partial}{\partial y}-y \frac{\partial}{\partial x} \) is a vecto

Answer 1

The vector field
`\(X = x \` frac
`{\partial}{\partial y} - y \` frac
`{\partial}{\partial x}\)` is a tangent vector to the paraboloid
`\(z = x^(2) + y^(2)\) in \(\mathbb{R}^(3)\).`

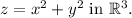
Step-by-step explanation:

To show that
`\(X\)\\` is a tangent vector to the paraboloid M, we can express
`\(X\)\\` in terms of the parametric equations of the paraboloid. The parametric representation of M is given by:

`\[ \mathbf{r}(u, v) = (u, v, u^(2) + v^(2)) \]`

Now, calculate the partial derivatives with respect to
`\(u\)` and
`\(v\):`

`\[ (\partial)/(\partial u) = \left(1, 0, 2u\right) \]`

`\[ (\partial)/(\partial v) = \left(0, 1, 2v\right) \]`

Now, express X in terms of these partial derivatives:

`\[ X = x (\partial)/(\partial y) - y (\partial)/(\partial x) = u(0, 1, 2v) - v(1, 0, 2u) = (-v, u, 0) \]`

This result shows that X is orthogonal to the normal vector of the surface, indicating that X is a tangent vector to the surface. Therefore, X is a tangent vector to the paraboloid M.