Question

Find a function f such that ∇f=⟨4yz,4xz,4xy+6z⟩. f=+K Use f to evaluate: ∫C​⟨4yz,4xz,4xy+6z⟩⋅dr= where C is the straight line from (−1,−1,3) to (1,1,5). Verify that the Fundamental Theorem of Line Integrals is correct by evaluating ∫C​⟨4yz,4xz,4xy+6z⟩⋅dr using the 16.2 method. C can be parametrized by: r(t)= (use the most natural parametrization) Express ∫C​⟨4yz,4xz,4xy+6z⟩⋅dr as an integral in terms of only t ∫C​⟨4yz,4xz,4xy+6z⟩⋅dr=∫ab​ where a= b= Evaluate the integral to get the same result as above:

Answer 1

To find a function f such that ∇f=⟨4yz,4xz,4xy+6z⟩, integrate each component of ∇f with respect to its corresponding variable. The resulting function is f(x,y,z) =
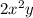`2x^2y`yz + 6xz + g(y,z) + h(x,z) + k(x,y), where g(y,z), h(x,z), and k(x,y) are arbitrary functions.

Step-by-step explanation:

To find a function f such that ∇f=⟨4yz,4xz,4xy+6z⟩, we integrate each component of ∇f with respect to its corresponding variable. Integrating 4yz with respect to x gives us 4xyz + g(y,z). Integrating 4xz with respect to y gives us 4xyz + h(x,z). Integrating 4xy+6z with respect to z gives us
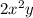`2x^2y` + k(x,y), where g(y,z), h(x,z), and k(x,y) are arbitrary functions of their respective variables. Therefore, f(x,y,z) =
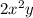`2x^2y` + 6xz + g(y,z) + h(x,z) + k(x,y), where g(y,z), h(x,z), and k(x,y) are arbitrary functions.