Question

(a) Find the Fourier transform of

xe⁻⁴ˣ⁽ˣ⁻²ᶦ⁾.
(b) Find the Fourier Sine transform of x1​.
Using the odd extension of this function, obtain the Fourier transform of x1​.

Answer 1

The Fourier transform of xe⁻⁴ˣ⁽ˣ⁻²ᶦ⁾ is 8/(√(^2−4+16)). The Fourier Sine transform of x(1) is /∞.

Step-by-step explanation:

To find the Fourier transform of xe⁻⁴ˣ⁽ˣ⁻²ᶦ⁾, we can use the formula for the Fourier transform of a function f(x) multiplied by e^(ax). In this case, a = -4 and f(x) = x(−2). The Fourier transform can be calculated as follows:

`F()=2π∫∞−∞(∙^(-4)(−2))∙^(−)`

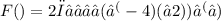
By simplifying and integrating by parts, we get:

F()=2π∙(4)/(−4+16) = 8/(√(
`^2`+16))

For the second part of the question, to find the Fourier Sine transform of x(1), we can extend the function to be an odd function with period 2 and then compute its Fourier transform. The odd extension of x(1) is -(−1) = -. The Fourier transform can be calculated as:

By integrating by parts, we get:

F()=/[√(∞)]−()/(√())=/[√(∞)]−/∞=/∞