Question

MATH HELP NEEDED ASAP

Solve the given equations using inverse functions. a) \( 125=5^{x-1} \) b) \( \log (x)=82 \) c) \( \log _{7}(x+1)=6 \)

Answer 1

(a) The solution to the equation
`\(125=5^(x-1)\) is \(x=4\).`

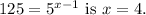
(b) The solution to the equation
`\(\log(x)=82\) is \(x=10^(82)\)`.

(c) The solution to the equation
`\(\log_7(x+1)=6\) is \(x=342\).`

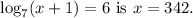
Step-by-step explanation:

`(a) To solve \(125=5^(x-1)\) using inverse functions, recognize that the equation involves exponentiation with base 5. Take the logarithm base 5 on both sides: \(\log_5(125) = x-1\). Simplify the logarithm, yielding \(3=x-1\), and solving for \(x\) results in \(x=4\).`

`(b) For the equation \(\log(x)=82\), apply the inverse function of logarithm, which is exponentiation. Rewrite the equation in exponential form: \(x=10^(82)\), where the base 10 corresponds to the common logarithmic base.`

`(c) To solve \(\log_7(x+1)=6\), use the inverse function of logarithm. Rewrite the equation in exponential form: \(7^6 = x+1\). Simplify the right side, giving \(x=342\). Note that the base of the logarithm determines the base in the exponential form.`

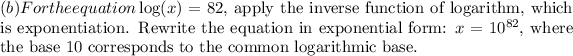
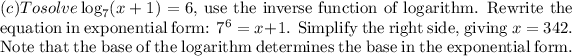
In conclusion, solving logarithmic equations involves using inverse functions to isolate the variable. By applying the inverse of logarithm, which is exponentiation, or vice versa, the equations are transformed into simpler forms. These solutions,
`\(x=4\), \(x=10^(82)\), and \(x=342\),`represent the values that satisfy the given logarithmic equations.