Question

X'(t) = ay(t) - a(2c-1)x(t) + bm(t)ᶜ

y'(t) = 2gm(t)x(t) - 2rx(t) - aᶜ(2-c)x(t) + cb*m(t)ᶜ
with initial conditions x(0) = 0, y(0) = 0,
and m(0) = v
C>=2
here is the solution for x(t) how did we get it and find y(t)
x(t)=x(0)ᵉ(-a(2c-1)t)+ a (intgration from 0 to t)ᵉ(-a(2c-1)(t-z) y(z) dz

Answer 1

The solution for x(t) can be found by integrating the given equation and using the initial conditions. The solution for y(t) cannot be determined without further information.

Step-by-step explanation:

The given solution for x(t) can be obtained by using the initial conditions and integrating the given equation. By solving the given equation, we can find that the solution for x(t) is:

`x(t) = x(0)e^(-a(2c-1)t) + a∫(0 to t)e^(-a(2c-1)(t-z))y(z)dz`

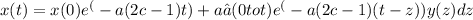
To find the solution for y(t), we need to integrate the given equation with respect to time and substitute the obtained values into the equation. However, the solution for y(t) is not provided in the question, so we cannot determine it without further information.