Question

The lines represented by the equations y + 5/3x = -4 and 3y - 5x = 9 are

the same line
parallel
neither parrallel nor perpendicular
perpendicular
SOMEONE PLS HELP

Answer 1

Neither parallel nor perpendicular

Explanation:

If two lines are parallel, they share the same slope. If two lines have slopes that are opposite reciprocals of each other, then they are perpendicular. If it is the same line, then the two equations must be the same when converted into the same form. If none of these apply, then the line is neither of any these.

1) First, convert each equation into y = mx + b format, or slope-intercept form, to easily identify their slopes. Isolate y in both equations.

First equation:

`y + (5)/(3) x = -4\\y = -(5)/(3) x-4`

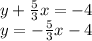
Second equation:

`3y - 5x = 9 \\3y = 5x + 9 \\y = (5)/(3) x + 3`

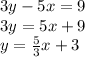
2) In slope-intercept format, the coefficient of the x term, or m, represents the slope. Thus, the slope of the first equation is
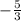`-(5)/(3)` while the slope of the second equation is
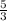`(5)/(3)`. The slopes are not the same, nor are they opposite reciprocals of each other. The equations are not the same either. Therefore, they are neither parallel nor perpendicular.

Answer 2

• C. neither parallel nor perpendicular

Explanation:

Given lines:

• y + 5/3x = -4 and 3y - 5x = 9

To determine the relationship between the lines put them both into slope-intercept form and compare the slopes.

• y + 5/3x = -4 ⇒ y = -5/3x - 4
• 3y - 5x = 9 ⇒ 3y = 5x + 9 ⇒ y = 5/3x + 3

The slopes are different so the lines are neither parallel nor perpendicular.

Correct choice is C