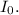The slit width is approximately
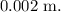 The intensity
The intensity
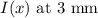 from the center is similar to
from the center is similar to
 due to small angle approximation in single-slit diffraction.
due to small angle approximation in single-slit diffraction.
The diffraction pattern produced by a single slit can be described by the single-slit diffraction formula, which gives the angular position of the minima:
![\[ \sin \theta_m = m \lambda / b \]](https://img.qammunity.org/2024/formulas/physics/high-school/ctj2g73hswpgjy0ugsoj9yic2s1rbbeav0.png)
where:
-
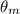 is the angle of the
is the angle of the
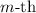 minimum,
minimum,
-
 is the order of the minimum (for the first minimum,
is the order of the minimum (for the first minimum,
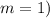 ,
,
-
 is the wavelength of the light,
is the wavelength of the light,
-
 is the slit width.
is the slit width.
The distance between the centers of adjacent minima on the screen is related to the angle
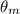 and the distance from the slit to the screen (\( L \)) by the equation:
and the distance from the slit to the screen (\( L \)) by the equation:
![\[ d_m = \frac{{2L \lambda}}{{b}} \sin \theta_m \]](https://img.qammunity.org/2024/formulas/physics/high-school/xcxvq0aksc0yfbdju83oc1l8yulpbvzeeo.png)
In this case, the given values are:
- Wavelength
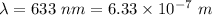
- Distance to the screen
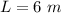
- Distance between minima
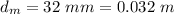
For the first minimum
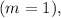 we can use the above equations to find the slit width
we can use the above equations to find the slit width
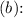
![\[ \sin \theta_1 = \frac{{\lambda}}{{b}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/6x3fdvo6ajb41uuqeb4zjqv4qy3sn2f7uz.png)
![\[ b = \frac{{\lambda}}{{\sin \theta_1}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/qpta4gadh4eoccrnn7285t7gbrddgrlz84.png)
![\[ b = \frac{{\lambda}}{{\sin \left(\arcsin\left(\frac{{d_1}}{{2L\lambda}}\right)\right)}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/7epq1irmq5qfp1u3bcrlqxhcfsbmyo7oym.png)
![\[ b = \frac{{\lambda}}{{\sqrt{{\frac{{d_1}}{{2L\lambda}}^2}}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/kk5p3nuiwvi56dzcyimtzxi9qwg0cdaif2.png)
![\[ b = \frac{{\lambda}}{{\sqrt{{\frac{{d_1^2}}{{4L^2\lambda^2}}}}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/vpufuyyki41nfmh8mkm4ocorpaetaupp62.png)
![\[ b = \frac{{\lambda}}{{\frac{{d_1}}{{2L\lambda}}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/th748f5fs5vpyp6fqrbeadhowdvekqb0el.png)
![\[ b = \frac{{2L\lambda^2}}{{d_1}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/oa7cw2uueako5m3559ywjtf9p9upfo8tgh.png)
Now, plug in the values:
![\[ b = \frac{{2 * 6 \ \text{m} * (6.33 * 10^(-7) \ \text{m})^2}}{{0.032 \ \text{m}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/kbd6flv6b966tk5g8jrdibef5s1lhgxaa9.png)
![\[ b \approx 0.002 \ \text{m} \]](https://img.qammunity.org/2024/formulas/physics/high-school/8hsz1at201oto8uj3imdbbmm06v5wzh574.png)
Now, to find the intensity at a position on the screen
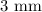 from the center of the pattern
from the center of the pattern
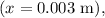 you can use the intensity formula for single-slit diffraction:
you can use the intensity formula for single-slit diffraction:
![\[ I(x) = I_0 \left(\frac{{\sin(\beta)}}{{\beta}}\right)^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/230iad93oxcdvmjsnz6ktuda1h916wnh0m.png)
where
 is the intensity at the center of the pattern, and
is the intensity at the center of the pattern, and
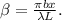
![\[ \beta = \frac{{\pi * 0.002 \ \text{m} * 0.003 \ \text{m}}}{{6.33 * 10^(-7) \ \text{m} * 6 \ \text{m}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/bo1m72g4woi9zr0xnugwd6cjycl1xqffgz.png)
![\[ \beta \approx 0.03 \]](https://img.qammunity.org/2024/formulas/physics/high-school/sbd0pnjrw2qwc5ac01a9x9nu8xnld4ubfm.png)
Now, calculate

![\[ I(x) = I_0 \left(\frac{{\sin(0.03)}}{{0.03}}\right)^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/bpt03no5v4s5y84hac7r2ek8vtzhrkn9r5.png)
Since
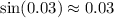 , the intensity will be close to
, the intensity will be close to
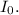 Therefore, the intensity at a position
Therefore, the intensity at a position
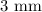 from the center of the pattern will be approximately the same as the intensity at the center,
from the center of the pattern will be approximately the same as the intensity at the center,