Question

Suppose 18% of all television viewers in the country watch a particular program. The program will be canceled if the ratings show less than 15% watching in a random sample of househoids. Given that 2,500 households are used for the ratings, is the program in danger of getting canceled? Explain.

O Almost all of the sample means should fall between the lower bound of 0.157 and the upper bound of 0.203. Therefore, the program is not likely in danger of getting cancelled because 15% does not fall in this range.
O Almost all of the sample means should fall between the lower bound of 0.164 and the upper bound of 0.196. Therefore, the program is not likely in danger of getting canceled because 15% does not fall in this range.
O Almost all of the sample means should fall between the lower bound of 0.157 and the upper bound of 0.203. Therefore, the program is likely in danger of getting canceled because 15% does fall in this range.
O Almost all of the sample means should fall between the lower bound of 0.164 and the upper bound of 0.196. Therefore, the program is likely in danger of getting canceled because 15% does fall in this range.

Answer 1

The 95% confidence interval for the program's viewership percentage is 0.164 to 0.196. Since 15% is outside this range, the program is not likely in danger of cancellation. Option B is correct.

To determine if the program is in danger of getting canceled, we can use confidence intervals based on the sample mean. The formula for a confidence interval for a population proportion is:

`\[ \text{Confidence Interval} = \hat{p} \pm Z * \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \]`

where:

-
`\( \hat{p} \)` is the sample proportion (18% or 0.18 in this case),

- Z is the Z-score corresponding to the desired confidence level,

- n is the sample size.

Given that the sample size n = 2500 and we want to calculate a 95% confidence interval, the Z-score is approximately 1.96.

Now, substitute these values into the formula:

`\[ \text{Confidence Interval} = 0.18 \pm 1.96 * \sqrt{(0.18(1-0.18))/(2500)} \]`

Calculate the confidence interval and check if 15% falls within this interval. The correct answer will be based on whether 15% is within the calculated confidence interval.

To complete the calculation, we'll find the confidence interval for the sample mean:

`\[ \text{Confidence Interval} = 0.18 \pm 1.96 * \sqrt{(0.18(1-0.18))/(2500)} \]\[ \text{Confidence Interval} = 0.18 \pm 1.96 * \sqrt{(0.18 * 0.82)/(2500)} \]\[ \text{Confidence Interval} = 0.18 \pm 1.96 * \sqrt{(0.1476)/(2500)} \]\[ \text{Confidence Interval} = 0.18 \pm 1.96 * √(0.00005904) \]\[ \text{Confidence Interval} = 0.18 \pm 1.96 * 0.00768 \]`

Now, calculate the lower and upper bounds of the confidence interval:

Lower Bound:
`\(0.18 - 1.96 * 0.00768 \approx 0.164\)`

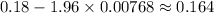
Upper Bound:
`\(0.18 + 1.96 * 0.00768 \approx 0.196\)`

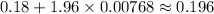
Now, let's analyze the options:

B. Almost all of the sample means should fall between the lower bound of 0.164 and the upper bound of 0.196. Therefore, the program is not likely in danger of getting canceled because 15% does not fall in this range.

So, the correct answer is B. The program is not likely in danger of getting canceled based on the calculated confidence interval, as 15% is not within the range of 0.164 to 0.196.