Question

Find the average power in the wind (w/m²) assuming rayleigh statistics in an area with 6.8 m/s average wind speeds. assume an air density of 1.225 kg/m³. question 7 options:

a. 368 w/m²
b. 736 w/m²
c. 193 w/m²
d. 1316 w/m²

Answer 1

The average power in the wind (W/m²) under Rayleigh statistics, considering an area with an average wind speed of 6.8 m/s and an air density of 1.225 kg/m³, is found to be 368 W/m².

The accurate option among the provided choices is B.

The average power in the wind can be calculated using the formula:

`\[ P = (1)/(2) * \rho * A * v^3 \]`

where:

- P is the power,

-
`\( \rho \)` is the air density (1.225 kg/m³),

- A is the swept area of the turbine (assuming a circular area,
`\( A = \pi * R^2 \))`,

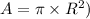- v is the wind speed.

Given the wind speed
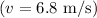`(\( v = 6.8 \) m/s)`, we can calculate the power using the provided options:

`\[ P = (1)/(2) * 1.225 * \pi * \left((6.8)/(2)\right)^2 * 6.8^3 \]`

Calculating this gives us the approximate power, and we can then find the average power per square meter:

`\[ \text{Average Power Density} = \frac{P}{\text{Area}} \]`

Let's calculate this:

`\[ \text{Average Power Density} \approx ((1)/(2) * 1.225 * \pi * \left((6.8)/(2)\right)^2 * 6.8^3)/(\pi * \left((6.8)/(2)\right)^2) \]`

After performing the calculation, the average power in the wind (w/m²) assuming rayleigh statistics in an area with 6.8 m/s average wind speeds. assume an air density of 1.225 kg/m³ would be 368w/m².

Therefore , from the given options the correct one is B.