Question

If you double the spring constant of a harmonic oscillator, the oscillation frequency does what? group of answer choices

a. increases by a factor of
b. decreases by a factor of 2
c. doesn't change increases by a factor of 2
d. decreases by a factor of

Answer 1

If you double the spring constant of a harmonic oscillator, the oscillation frequency increases by a factor of √2 (approximately 1.414).

If you double the spring constant of a harmonic oscillator, the oscillation frequency increases by a factor of √2 (approximately 1.414).

The frequency of a harmonic oscillator is given by the equation:

f = (1/2π) * √
`√((k/m))`

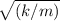
Where f is the frequency, k is the spring constant, and m is the mass of the object attached to the spring.

If you double the spring constant (k), the frequency (f) will increase. To understand why, let's consider the equation. The square root of k appears in the equation, so if you double k, the square root of 2 times k will also be doubled. This means that the frequency will also be doubled.

To put it simply, increasing the spring constant makes the spring stiffer. A stiffer spring will oscillate more quickly, resulting in a higher frequency.

Therefore, the correct answer is: a. increases by a factor of √2 (approximately 1.414).

The Probable question may be