The block's final speed is
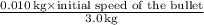 after a 10-g bullet penetrates a 3.0-kg wood block, coming to rest.
after a 10-g bullet penetrates a 3.0-kg wood block, coming to rest.
To solve this problem, we can use the principle of conservation of linear momentum. The total linear momentum before the collision is equal to the total linear momentum after the collision.
The linear momentum (p) is given by the product of mass and velocity
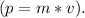
Before the collision:
![\[ \text{Momentum of bullet} = m_{\text{bullet}} * v_{\text{bullet\_initial}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/fil8i5tgu1zfai7mbeabl8e16u1fos0w5u.png)
![\[ \text{Momentum of block} = m_{\text{block}} * v_{\text{block\_initial}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/oijkgbkeyemx5w4x35dqp4ejltdn58g0n0.png)
After the collision:
![\[ \text{Momentum of bullet} = m_{\text{bullet}} * v_{\text{bullet\_final}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/jvcoy83o3d28e3ce2tubtchz23nikzgsi1.png)
![\[ \text{Momentum of block} = m_{\text{block}} * v_{\text{block\_final}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/hwusoavbhiz38tjd94katyn7hmeqogsb82.png)
The total linear momentum before the collision is equal to the total linear momentum after the collision:
![\[ m_{\text{bullet}} * v_{\text{bullet\_initial}} + m_{\text{block}} * v_{\text{block\_initial}} = m_{\text{bullet}} * v_{\text{bullet\_final}} + m_{\text{block}} * v_{\text{block\_final}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/7e8q84rxco0t8lljzfs55w7ggtig8c7q8e.png)
Now, substitute the given values:
![\[ (0.010 \, \text{kg}) * v_{\text{bullet\_initial}} + (3.0 \, \text{kg}) * 0 = (0.010 \, \text{kg}) * 0 + (3.0 \, \text{kg}) * v_{\text{block\_final}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/4u8r4pm7quvw2dlvpacy243zou4wda041v.png)
Since the block is initially at rest
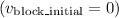 and the bullet comes to rest after penetrating the block
and the bullet comes to rest after penetrating the block
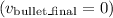 , the equation simplifies to:
, the equation simplifies to:
![\[ (0.010 \, \text{kg}) * v_{\text{bullet\_initial}} = (3.0 \, \text{kg}) * v_{\text{block\_final}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/ed72rrf4311k7hkthdcj3z3vo5frz69u0c.png)
Now, solve for \(v_{\text{block\_final}}\):
![\[ v_{\text{block\_final}} = \frac{0.010 \, \text{kg} * v_{\text{bullet\_initial}}}{3.0 \, \text{kg}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/sql6fmyr2iy36c4wv6o9lrwejprwddh0io.png)
Insert the given value for
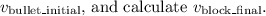
Note: Make sure to use consistent units, and the final result will be in meters per second (m/s).