Question

given are n independent measurements n v 1 ,... v n of the noise voltage v at a certain point in a receiver. the noise v is a gaussian random variable with unknown mean and unknown variance. work out the maximum-likelihood estimators for the unknown parameters based on n measurements. calculate theexpected values of these estimates as functions of true parameters

Answer 1

The maximum likelihood estimators for a Gaussian random variable with unknown mean and variance are the sample mean and biased sample variance. The expected values are the true mean and a biased estimate of the true variance.

In the context of a Gaussian random variable with unknown mean
`(\(\mu\))` and unknown variance
`(\(\sigma^2\))`, the likelihood function is given by the product of the probability density functions (PDFs) of the individual measurements. The probability density function for a Gaussian distribution is given by:

`\[ f(v_i; \mu, \sigma^2) = (1)/(√(2\pi\sigma^2)) e^{-((v_i - \mu)^2)/(2\sigma^2)} \]`

The likelihood function (L) for n independent measurements is the product of the individual PDFs:

`\[ L(\mu, \sigma^2) = \prod_(i=1)^(n) (1)/(√(2\pi\sigma^2)) e^{-((v_i - \mu)^2)/(2\sigma^2)} \]`

To find the maximum likelihood estimators (MLEs), we take the partial derivatives of the logarithm of the likelihood function with respect to
`\(\mu\)` and
`\(\sigma^2\)`, set them to zero, and solve for the parameters.

1. MLE for
`\(\mu\)`:

`\[ (\partial \ln L)/(\partial \mu) = (1)/(\sigma^2) \sum_(i=1)^(n) (v_i - \mu) = 0 \]`

Solving for
`\(\mu\)`, we get:

`\[ \hat{\mu} = (1)/(n) \sum_(i=1)^(n) v_i \]`

The MLE for the mean
`(\(\mu\))` is the sample mean.

2. MLE for
`\(\sigma^2\)`:

`\[ (\partial \ln L)/(\partial (\sigma^2)) = -(n)/(2\sigma^2) + (1)/(2\sigma^4) \sum_(i=1)^(n) (v_i - \mu)^2 = 0 \]`

Solving for
`\(\sigma^2\)`, we get:

`\[ \hat{\sigma^2} = (1)/(n) \sum_(i=1)^(n) (v_i - \hat{\mu})^2 \]`

The MLE for the variance
`(\(\sigma^2\))` is the sample variance.

Now, let's calculate the expected values of these estimates as functions of the true parameters:

1. Expected value of
`\(\hat{\mu}\)`:

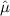`\[ E(\hat{\mu}) = E\left((1)/(n) \sum_(i=1)^(n) v_i\right) = (1)/(n) \sum_(i=1)^(n) E(v_i) \]`

Since v is a Gaussian random variable,
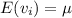`\(E(v_i) = \mu\)`, so:

`\[ E(\hat{\mu}) = (1)/(n) \sum_(i=1)^(n) \mu = \mu \]`

The expected value of the sample mean is the true mean
`(\(\mu\))`.

2. Expected value of
`\(\hat{\sigma^2}\)`:

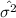`\[ E(\hat{\sigma^2}) = E\left((1)/(n) \sum_(i=1)^(n) (v_i - \hat{\mu})^2\right) \]`

Expanding this expression involves moments of the distribution and is more complex, but it can be shown that:

`\[ E(\hat{\sigma^2}) = (n-1)/(n) \sigma^2 \]`

The expected value of the sample variance is a biased estimator of the true variance.

In summary, the maximum likelihood estimators for the unknown parameters are the sample mean
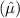`(\(\hat{\mu}\))` and the biased sample variance
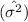`(\(\hat{\sigma^2}\))`. The expected value of the sample mean is the true mean
`(\(\mu\))`, and the expected value of the sample variance is a biased estimator of the true variance
`(\(\sigma^2\))`.