Question

An owl flying at 27 m/s emits a cry whose frequency is 440 hz. a mockingbird is moving in the same direction as the owl at 13 m/s. (assume the speed of sound is 343 m/s.)

what frequency does the mockingbird hear (in hz) as the owl approaches the mockingbird? hz

Answer 1

As the owl (440 Hz) approaches the mockingbird at 13 m/s, with both moving in the same direction, the mockingbird hears an observed frequency of approximately 423.78 Hz due to Doppler effect.

To find the frequency heard by the mockingbird as the owl approaches, we can use the Doppler effect formula for frequency:

`\[ f' = (f \cdot (v + v_0))/((v + v_s)) \]`

where:

-
`\( f' \)` is the observed frequency (heard by the mockingbird),

-
`\( f \)` is the source frequency (emitted by the owl),

-
`\( v \)` is the speed of sound in air (343 m/s),

-
`\( v_0 \)`is the velocity of the observer (mockingbird) relative to the medium (air),

-
`\( v_s \)` is the velocity of the source (owl) relative to the medium.

In this case, the owl and the mockingbird are moving in the same direction, so their relative velocity
`(\(v_s - v_0\))` is the difference of their individual velocities.

Given:

-
`\( f = 440 \, \text{Hz} \)` (frequency of the owl's cry),

-
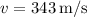`\( v = 343 \, \text{m/s} \)`(speed of sound),

-
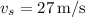`\( v_s = 27 \, \text{m/s} \)` (velocity of the owl),

-
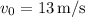`\( v_0 = 13 \, \text{m/s} \)` (velocity of the mockingbird),

Substitute these values into the formula:

`\[ f' = (440 \cdot (343 + 13))/((343 + 27)) \]`

Now, calculate the observed frequency:

`\[ f' = (440 \cdot 356)/(370) \]`

`\[ f' \approx 423.78 \, \text{Hz} \]`

So, the mockingbird hears a frequency of approximately
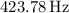`\( 423.78 \, \text{Hz} \)` as the owl approaches.