The correlation between these two variables, number of ads and increased sales is equal to 0.9909.
In Mathematics, the Pearson product-moment correlation coefficient (r) can be modeled by the following mathematical equation;

Where:
- r represents the correlation coefficient.
- x is the independent variable in a sample.
 is the mean of the independent variable.
is the mean of the independent variable.- x is the dependent variable in a sample.
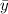 is the mean of the dependent variable.
is the mean of the dependent variable.
Next, we would calculate the mean of the the independent variable (x-variable) and dependent variable (y-variable) as follows;
Mean,
 = [∑(x)]/n
= [∑(x)]/n
Mean,
 = (16 + 12 + 18 + 14)/4
= (16 + 12 + 18 + 14)/4
Mean,
 = 15
= 15
Mean,
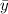 = [∑(y)]/n
= [∑(y)]/n
Mean,
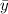 = (330 + 270 + 380 + 300)/4
= (330 + 270 + 380 + 300)/4
Mean,
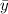 = 320
= 320
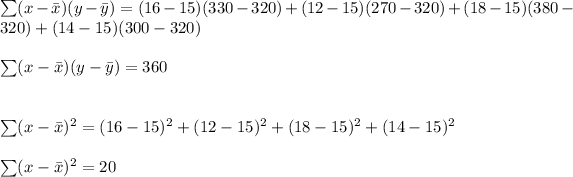
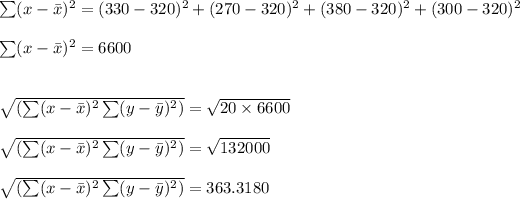
Now, we can calculate the Pearson product-moment correlation coefficient;
Correlation coefficient, r = 360/363.3180
Correlation coefficient, r = 0.9909.