Question

Find a general solution to the differential equation y' =(x ²−4)(3y+2)using the method of separation of variables.

Answer 1

The general solution to the differential equation y' =(x²-4)(3y+2) is obtained by separating variables, integrating both sides, and then solving for y, which will include a constant of integration C.

Step-by-step explanation:

To find a general solution to the differential equation y' =(x²-4)(3y+2) using the method of separation of variables, follow these steps:

1. Separate the variables by dividing both sides by (3y+2) and then integrating both sides, which gives:
2. 
   `\int (1)/(3y+2) dy = \int (x²-4) dx`
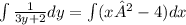
3. Integrate both sides:
4. 
   `(1)/(3) \ln|3y+2| = (1)/(3)x³ - 4x + C`
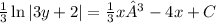
5. Solve for y to get the general solution:
6. 
   `y = (1)/(3) e^{3((1)/(3)x³ - 4x + C)} - (2)/(3)`

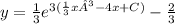
Note that C is the constant of integration and can represent any real number.