Question

a freight car with a mass of 25 000 kg rolls down an inclined track through a vertical distance of 1.5 m. at the bottom of the incline, on a level track, the car collides and couples with an identical freight car that was at rest. what percentage of the initial kinetic energy is lost in the collision?

Answer 1

50% of the initial kinetic energy is lost in the collision.

The initial kinetic energy of the freight car is equal to the potential energy it gained while rolling down the incline. This potential energy (PE) is given by:

PE = mgh

So, the initial kinetic energy is:

`$KE_{\text{initial}} = mgh = 25,000 \, \text{kg} * 9.81 \, \text{m/s}^2 * 1.5 \, \text{m} = 367,875 \, \text{J}$$`

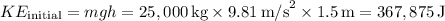
After the collision, the two cars move together as one object with a combined mass of 50,000 kg. The final kinetic energy is given by:

`$KE_{\text{final}} = (1)/(2) M v^2$$`

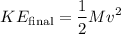
The final velocity can be found using conservation of momentum:

`$m_1v_1 + m_2v_2 = (m_1 + m_2)v$$`

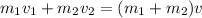
Since the second car was initially at rest,
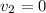`$v_2 = 0$`, and since the two cars have the same mass,
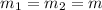`$m_1 = m_2 = m$`, we get:

`$mv + 0 = 2mv \Rightarrow v = (v_1)/(2)$$`

Substituting this into the equation for
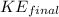`KE_{final` gives:

`$KE_{\text{final}} = (1)/(2) * 2m * \left((v_1)/(2)\right)^2 = (1)/(2) m v_1^2 = (1)/(2) KE_{\text{initial}}$$`

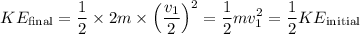
The percentage of the initial kinetic energy lost in the collision is then given by:

`$\text{Percentage loss} = \frac{KE_{\text{initial}} - KE_{\text{final}}}{KE_{\text{initial}}} * 100\% = \frac{KE_{\text{initial}} - (1)/(2) KE_{\text{initial}}}{KE_{\text{initial}}} * 100\% = 50\%$$`

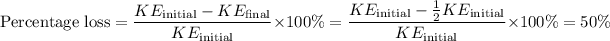
So, 50% of the initial kinetic energy is lost in the collision.