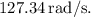The angular velocity of the propeller is approximately
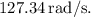
To find the angular velocity
 in radians per second, you can use the formula:
in radians per second, you can use the formula:
![\[ \omega = \frac{2\pi * \text{revolutions}}{\text{time}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/dfywfu4230cx9em4pf9gjyb3fclgpg5tec.png)
Given that the propeller spins at 1220 revolutions per minute, you can plug in the values:
![\[ \omega = \frac{2\pi * 1220 \text{ rev/min}}{1 \text{ min}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/jsbah1pcm361ok9yl391claecljcctti95.png)
Now, you need to convert minutes to seconds because there are 60 seconds in a minute:
![\[ \omega = \frac{2\pi * 1220 \text{ rev}}{1 \text{ min}} * \frac{1 \text{ min}}{60 \text{ s}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/lj4nv1ooujwtik3qtkzho4467bi2t296hv.png)
Simplify the expression:
![\[ \omega = (2\pi * 1220)/(60) \text{ rad/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/4cgqjiw2kmfzzjlezvwauezo7sgpjbt4bf.png)
Now, calculate the value:
![\[ \omega = (2 * 3.1416 * 1220)/(60) \]](https://img.qammunity.org/2024/formulas/physics/high-school/o8ny2o28qljpjtnop3wakuznt5y47g41ae.png)
![\[ \omega \approx (7640.48)/(60) \]](https://img.qammunity.org/2024/formulas/physics/high-school/pz8hr60oplbmwtarwer6nnun89vsc6fjt0.png)
![\[ \omega \approx 127.34 \, \text{rad/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/jn9do8apc582a1uziz19ieqjwfmuq6a5f0.png)
So, the angular velocity of the propeller is approximately