Question

a certain elastic conducting material is stretched into a cir- cular loop of 12.0 cm radius. it is placed with its plane perpendicular to a uniform 0.800 t magnetic field. when released, the ra- dius of the loop starts to shrink at an instantaneous rate of 75.0 cm/s. what emf is induced in the loop at that instant?

Answer 1

The induced emf in the loop at that instant is approximately -0.942 V (the negative sign indicates the direction of the induced current).

To find the induced electromotive force (emf) in the loop, we can use Faraday's law of electromagnetic induction, which states that the emf induced in a closed loop is equal to the rate of change of magnetic flux through the loop.

Given:

Radius of the circular loop (initial) = 12.0 cm = 0.12 m

Rate of change of radius = -75.0 cm/s = -0.75 m/s (negative sign indicates shrinking)

First, let's find the rate of change of magnetic flux through the loop:

The magnetic flux through a circular loop is given by the formula Φ = B * A, where B is the magnetic field strength and A is the area of the loop.

The area of the circular loop is A = π * r^2, where r is the radius of the loop.

Initial area of the loop = π *
`(0.12 m)^2`

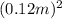
Final area of the loop = π * (r - Δr)^2, where Δr is the change in radius

The rate of change of magnetic flux is:

ΔΦ/Δt = (π * (r - Δr)^2 - π * r^2) / Δt

= π * (r^2 - 2 * r * Δr + Δr^2 - r^2) / Δt

= π * (2 * r * Δr - Δr^2) / Δt

Now, we can find the induced emf using Faraday's law:

emf = -dΦ/dt, where dΦ/dt is the rate of change of magnetic flux

emf = -π * (2 * r * Δr - Δr^2) / Δt

Substituting the given values:

emf = -π * (2 * 0.12 m * (-0.75 m/s) -
`(-0.75 m/s)^2)` / (-0.75 m/s)

emf = -π * (2 * 0.12 m * 0.75 m/s -
`(0.75 m/s)^2`) / (0.75 m/s)

Simplifying the equation, we find:

emf ≈ -π * (2 * 0.12 m * 0.75 m/s -
`(0.75 m/s)^2` / (0.75 m/s)