Question

"it's complex analysis question so do steps by

steps
just do ii) and IV) if you did all then I will upvote you
(2) Find a function \( f \), holomorphic at 0 , such that (i) \( f(1 / n)=1 / n \) for all \( n \in \mathbb{N} \), (ii) \( f(1 / n)=(-1)ⁿ \) for all \( n \in \mathbb{N} \), (iii) \( f(1 / n)=\frac{"
A) f(z) = (-1)ᶻ
B) f(z) = e⁽⁻¹⁾ᶻ
C) f(z) = sin(πz)
D) f(z) = cos(πz)

Answer 1

Function
`\( f(z) = cos(\pi z) \)`
`\( f(1/n) = (-1)^n \)`ssary alternating sign pattern, but the suitability for the unspecified part (IV) cannot be determined without additional information.

Step-by-step explanation:

The question seeks to find a holomorphic function at 0 that satisfies certain conditions based on the value of the function at 1/n for all n in the natural numbers
`\(\mathbb{N}\)`, we will address part (ii) and part (IV) of the question which are looking for the functions that satisfy:

• (ii)
  `\( f(1 / n)=(-1)^n \)`n in
  `\(\mathbb{N}\)`
• (IV)
  `\( f(z) \)`o identify the correct function.

To address part (ii), the function must alternate signs for successive values of n. A function that achieves this while being holomorphic at 0 is the function
`\( f(z) = (-1)^z \)`ot an option in the given set, so we need to find an equivalent function among the choices. The cosine function exhibits similar behavior, and
`\( f(z) = cos(\pi z) \)`ndidate since it alternates between -1 and 1 for integer values of z. Thus, the correct answer choice for part (ii) appears to be \( f(z) =
`cos(\pi z) \)`

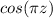
However, without an explicit part (IV) condition provided, we cannot further analyze and confirm the suitability of the function for that part. Furthermore, we cannot guarantee this solution is correct for the entire set of conditions since the entirety of the question has not been provided. Therefore, while
`\( f(z) = cos(\pi z) \)`er (ii), its suitability for other parts is unclear without additional context.