Final Answer:
A) The radius of convergence of the power series is
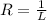 .
.
B) The power series converges for
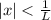 .
.
C) The power series converges for
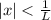 .
.
D) The power series converges absolutely for
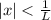 .
.
Step-by-step explanation:
The radius of convergence, R , is related to the limit L by the formula
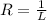 . This relationship arises from the fact that R is the reciprocal of the limit L as n approaches infinity. As L is the limit of
. This relationship arises from the fact that R is the reciprocal of the limit L as n approaches infinity. As L is the limit of
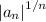 , taking the reciprocal gives
, taking the reciprocal gives
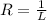 . This implies that the power series converges for values of x within a radius
. This implies that the power series converges for values of x within a radius
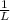 around the center of the series.
around the center of the series.
It's important to note that the convergence of a power series is guaranteed within its radius of convergence. Therefore, the power series converges for
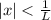 . This is because the distance from x to the center of the series, 0 , must be less than the radius of convergence for the series to converge. Thus, the correct statement is option B.
. This is because the distance from x to the center of the series, 0 , must be less than the radius of convergence for the series to converge. Thus, the correct statement is option B.
The absolute convergence of the power series is also determined within its radius of convergence. Since
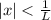 , the power series converges absolutely for
, the power series converges absolutely for
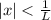 . Absolute convergence ensures convergence regardless of the sign of the terms in the series, providing a stronger form of convergence compared to conditional convergence. Therefore, option D is accurate.
. Absolute convergence ensures convergence regardless of the sign of the terms in the series, providing a stronger form of convergence compared to conditional convergence. Therefore, option D is accurate.