Question

What is the molecular formula for a compound that is 44.87% potassium, 36.7%

oxygen, 18.0% sulfur and a molecular mass of 696g.

Answer 1

Molecular formula: S4K8O16 empirical formula: SK2O4

Step-by-step explanation:

First we find the moles of each by first finding grams (using the percent) and then using stoichiometry to convert into moles:

Sulfur: 696 *.18 = 125.28grams S*
`(1 mole S)/(32.065 g S) = 3.907 moles S`

Potassium: 696 *.4487 = 312.2952 *
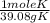`(1 mole K)/(39.08 g K)`= 7.99117 mole K

Oxygen: 696 * .367 = 255.432 *
`(1 mol O)/(16g O)` = 15.9654 mole O

Then we divide each value by the atom with the smallest number of moles to find the mole ratio:

3.907/3.907= 1

7.99117 mole K/ 3.907= 2.043

15.9654 mole O/ 3.907= 4.08

The empirical formula is SK2O4

To find the molecular formula, we divide the mass given (696) by the mass of the empirical formula (174.22) to get 4. We then divide each atom by 4.

Molecular formula: S4K8O16