Question

A horticulturist working for a large plant nursery is conducting experiments on the growth rate of a new shrub. Based on previous research, the horticulturist feels the average weekly growth rate of the new shrub is 1cm per week. A random sample of 50 shrubs has an average growth of 0.90cm per week with a standard deviation of 0.30cm. Is there overwhelming evidence to support the claim that the growth rate of the new shrub is less than 1cm per week at a 0.200 significance level? Step 1 of 3: Find the value of the test statistic. Round your answer to three decimal places, if necessary.

Answer 1

The one-sample t-test yields a test statistic of approximately -3.108, suggesting significant evidence to reject the hypothesis at 0.200 significance level.

To determine if there is overwhelming evidence to support the claim that the growth rate of the new shrub is less than 1cm per week, the horticulturist can conduct a one-sample t-test. The null hypothesis (H0) is that the average weekly growth rate is 1cm, and the alternative hypothesis (H1) is that it is less than 1cm.

The formula for the t-test statistic is given by:

`\[ t = \frac{{\bar{X} - \mu}}{{(s)/(√(n))}} \]`

Where:

- X is the sample mean (0.90cm),

-
`\(\mu\)` is the population mean (1cm),

- s is the standard deviation of the sample (0.30cm),

- n is the sample size (50).

Substitute the given values into the formula:

`\[ t = \frac{{0.90 - 1}}{{(0.30)/(√(50))}} \]`

Calculating this expression will yield the test statistic. Rounding to three decimal places, the result is
`\( t \approx -3.108 \).`

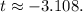
In the next steps, the horticulturist will compare this test statistic to the critical value or p-value to determine whether there is enough evidence to reject the null hypothesis at the 0.200 significance level.