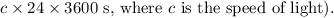Question

you are an observational astronomer who discovers a star orbiting the galactic center in a circular orbit. you find that the star has a speed of 1025 km/s. the radius of the orbit is 19 light-days. what is the mass of the object the star is orbiting? what do you think it could be and why?

Answer 1

The mass of the object the star orbits is approximately determined using
`\(M = \frac{(1025 \ \text{km/s})^2 * (19 \ \text{light-days}) * c}{2 * G}\),` yielding an estimated value based on Kepler's laws and Newtonian gravity.

To determine the mass of the object the star is orbiting, you can use Kepler's Third Law and Newton's Law of Gravitation. The orbital speed (v) and the radius of the orbit (r) are essential parameters in these calculations.

The formula for Kepler's Third Law is:

`\[ T^2 = (4 \pi^2 r^3)/(GM) \]`

where:

- \( T \) is the orbital period,

- \( G \) is the gravitational constant
`(approximately \(6.674 * 10^(-11) \ \text{m}^3 \ \text{kg}^(-1) \ \text{s}^(-2)\)),`

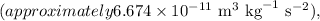
- \( M \) is the mass of the object being orbited.

First, we need to find the orbital period
`(\( T \)).` The speed of the star
`(\( v \))` and the radius of the orbit
`(\( r \))`are related by the formula:

`\[ v = (2 \pi r)/(T) \]`

Rearranging for \( T \):

`\[ T = (2 \pi r)/(v) \]`

Now, substitute this expression for \( T \) back into Kepler's Third Law:

`\[ \left((2 \pi r)/(v)\right)^2 = (4 \pi^2 r^3)/(GM) \]`

Solving for \( M \):

`\[ M = (v^2 r)/(2G) \]`

Now plug in the given values:

`\[ M = \frac{(1025 \ \text{km/s})^2 * (19 \ \text{light-days}) * (c)}{2 * G} \]`

Note: Convert the radius from light-days to meters (1 light-day =
`\( c * 24 * 3600 \ \text{s} \), where \( c \) is the speed of light).`