Question

Find the first four nonzero terms of the Taylor series about 0 for the function f(x) = arcsin(x). Note that you may want to find these in a manner other than by direct differentiation of the function.

Answer 1

The first four nonzero terms of the Taylor series for
`\(f(x) = \arcsin(x)\)` about x = 0 are x, as higher-order derivatives at x = 0 contribute terms that are zero or involve
`\(x^2\)` and higher powers.

To find the Taylor series for the function
`\(f(x) = \arcsin(x)\)` about x = 0, we can use the Maclaurin series expansion. The general formula for the Maclaurin series of f(x) is:

`\[ f(x) = f(0) + f'(0)x + (f''(0)x^2)/(2!) + (f'''(0)x^3)/(3!) + \ldots \]`

For
`\(f(x) = \arcsin(x)\)`, the derivatives at x = 0 are as follows:

`\(f(0) = \arcsin(0) = 0\)\\\(f'(x) = (1)/(√(1-x^2))\) and \(f'(0) = 1\)\\\(f''(x) = (x)/((1-x^2)^(3/2))\) and \(f''(0) = 0\)\\\(f'''(x) = (3x^2)/((1-x^2)^(5/2))\) and \(f'''(0) = 0\)`

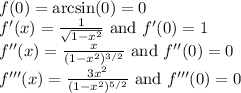
So, the Maclaurin series up to the third degree is:

`\[ \arcsin(x) \approx 0 + 1 \cdot x + 0 \cdot (x^2)/(2!) + 0 \cdot (x^3)/(3!) \]`

Simplifying, we get the first four nonzero terms:

`\[ \arcsin(x) \approx x \]`

Therefore, the first four nonzero terms of the Taylor series for
`\(f(x) = \arcsin(x)\)` about x = 0 are x.