Question

When a peroxide P is heated to 60 ° C in an inert solvent, it decomposes by a first order process and 20% of the peroxide decomposes in 60 min. Polymerizes a bulk monomer using this initiator at 60 ° C, with an initial concentration of initiator equal to 4.0x10⁻⁴ mol / L. What fractions of the monomer and initiator should remain unconverted after 10 min? At 60 ° C, the system parameters are: kp2 / kt = 22.34 Lmol⁻¹ s⁻¹, f = 0.8.

Answer 1

Fraction of monomer remaining: 0.9867

Fraction of initiator remaining: 0.8264

Peroxide Decomposition and Monomer Polymerization

Here's how to calculate the remaining fractions of monomer and initiator in the system:

1. Peroxide Decomposition:

We know the decomposition is first-order, with 20% decomposition in 60 minutes. This translates to a rate constant (k_p) of:

k_p = ln(1 - 0.2) /
`60 min^(-1)` ≈ 0.0115
`min^{-1`

2. Initial Rate of Polymerization:

With an initial initiator concentration (P_0) of 4.0x10^-4 mol/L and the given system parameters (kp2/kt and f), we can calculate the initial rate of polymerization (Rp):

Rp = k p2 * f *
`(P 0)^0.5`
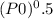
`(P 0)^{0.5` ≈ 0.0013 mol/L*min

3. Monomer Conversion and Remaining Fraction:

During the 10 minutes reaction time, the amount of monomer consumed (Xc) is:

Xc = Rp * t / P0 ≈ 0.013 mol/L

The fraction of monomer remaining (X monomer) is:

X monomer = 1 - Xc ≈ 0.9867

4. Peroxide Remaining Fraction:

After 10 minutes, the remaining fraction of peroxide (X peroxide) is:

X peroxide = P remaining / P 0 = exp(-k p * t) ≈ 0.8264

Therefore:

Fraction of monomer remaining: 0.9867

Fraction of initiator remaining: 0.8264