Question

Let L be the linear transformation defined in excercise 2, section 6.3.

Find teh transition matrix P from S' to S.

Answer 1

To find L's representation in basis T, convert the standard basis vectors (S) to T using the transition matrix, then reflect them using L's representation in S, and finally convert back to S using the inverse transition.

The problem is stated as follows:

Let
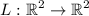`$L:\mathbb{R}^(2)\rightarrow\mathbb{R}^(2)$` be the linear transformation defined by a reflection about the x-axis. Let S be the standard basis and T be the ordered basis

`\[T=([\begin{matrix}1\\ 1\end{matrix}],[\begin{matrix}-1\\ 1\end{matrix}]).\]`

(a) Find the representation of L concerning S.

(b) Find the transition matrix P from T to S.

(c) Use your answer in part (c) and the material from Section 6.5 to find the representation of L concerning T. (Remember that you can check your answer by finding the representation of L concerning T directly.)

To solve this problem, we can first find the matrix representation of L concerning the standard basis S. This matrix will be of the form

`\[\begin{pmatrix} a & b \\ c & d \end{pmatrix}\]`

where a, b, c, and d are the coefficients that, when multiplied by the basis vectors of S, produce the reflected vectors. We can then find the transition matrix P from T to S, which will be of the form

`\[\begin{pmatrix} p_1 & p_2 \\ q_1 & q_2 \end{pmatrix}\]`

where
`$p_1$, $p_2$, $q_1$`, and
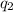`$q_2$` are the coefficients that, when multiplied by the basis vectors of T, produce the basis vectors of S. Finally, we can use the formula
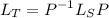`$L_T = P^(-1) L_S P$` to find the representation of L concerning T.

Once we have found the representation of L concerning T, we can check our answer by finding the representation of L concerning T directly. This should give us the same matrix that we obtained from part (c).