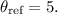For each angle:
1.
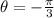 is in Quadrant III with
is in Quadrant III with
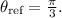
2.
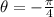 is in Quadrant III with
is in Quadrant III with
 .
.
3
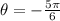 is in Quadrant III with
is in Quadrant III with
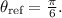
4.
 is in Quadrant I with
is in Quadrant I with
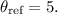
1.
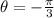
This angle is in Quadrant III (Negative x-axis, Negative y-axis).
The reference angle
 is
is
 .
.
2.
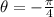
Also in Quadrant III (Negative x-axis, Negative y-axis).
The reference angle
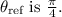
3.
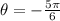
Once more, in Quadrant III (Negative x-axis, Negative y-axis).
The reference angle
 .
.
4.

This angle is in Quadrant I (Positive x-axis, Positive y-axis).
As it's already in the first quadrant, the reference angle
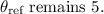
Hence:
1.
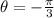 is found in Quadrant III with
is found in Quadrant III with
 .
.
2.
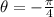 is found in Quadrant III with
is found in Quadrant III with
 .
.
3.
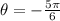 is found in Quadrant III with
is found in Quadrant III with
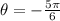
4.
 is found in Quadrant I with
is found in Quadrant I with