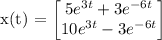(a) The eigenvalues are
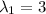 and
and
 and the corresponding eigenvectors are
and the corresponding eigenvectors are
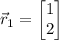 and
and
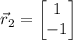 .
.
(b) The real form is:
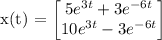
The initial value problem is:
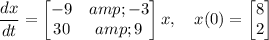
(a) We need to find the eigenvalues and eigenvectors for the coefficient matrix. The eigenvalues are
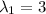 and
and
 , and the corresponding eigenvectors are
, and the corresponding eigenvectors are
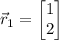 and
and
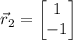 .
.
(b) To solve the initial value problem, we can use the general solution of the homogeneous equation:
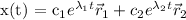
Then we can use the initial condition to find the values of
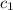 and
and
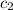 . Substituting t = 0
. Substituting t = 0
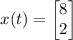 into the general solution, we get the system of equations:
into the general solution, we get the system of equations:

Solving this system, we find that $c_1 = 5$ and $c_2 = 3$. Therefore, the solution to the initial value problem is:

In real form, this is: