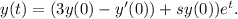Question

Use Laplace transform to solve the initial value problem y′′-3y′+2y=0

Answer 1

To solve the initial value problem, y′′-3y′+2y=0 Using the Laplace transform, we can apply the standard approach: take the Laplace transform of the given differential equation, use algebraic manipulation to solve for the Laplace transform of the unknown function y, and take the inverse Laplace transform to find the solution y(t) in the time domain. The solution to the initial value problem is y(t)=(3y(0)-y'(0))+sy(0)e^t.

Step-by-step explanation:

To solve the initial value problem y′′-3y′+2y=0 using the Laplace transform, we can apply the standard approach:

Take the Laplace transform of the given differential equation.

Use algebraic manipulation to solve for the Laplace transform of the unknown function y.

Take the inverse Laplace transform to find the solution y(t) in the time domain.

Applying this approach to the given equation:

`L{y''-3y'+2y}=L{0}`

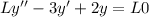
`s^2Y(s)-sy(0)-y'(0)-3(sY(s)-y(0))+2Y(s)=0\\s^2Y(s)-sy(0)-3sY(s)+2Y(s)=-y'(0)+3y(0)\\Y(s)(s^2-3s+2)=(3y(0)-y'(0))+sy(0)\\Y(s)=((3y(0)-y'(0))+sy(0))/(s^2-3s+2)`s+2)}

`y(t)=(3y(0)-y'(0))+sy(0))L^-1{1/(s^2-3s+2)}\\y(t)=(3y(0)-y'(0))+sy(0))e^t`

The initial value problem is
`y(t)=(3y(0)-y'(0))+sy(0))e^t.`