Question

Find the solution to the given differential equation.
y′′+8y′+16y=0

Answer 1

The solution to the differential equation y''+8y'+16y=0 is
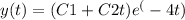`y(t) = (C1 + C2t)e^(-4t)`the characteristic equation and considering the repeated root r = -4.

Step-by-step explanation:

The differential equation in question is y'' + 8y' + 16y = 0. This is a second-order linear homogeneous differential equation with constant coefficients. To solve it, we look for solutions of the form y = e^(rt), where r is a constant that satisfies the characteristic equation.

The characteristic equation is
`r^2 + 8r + 16 = 0` ctored as
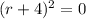`(r + 4)^2 = 0`us a repeated root of r = -4. Therefore, the general solution to the differential equation is
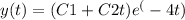`y(t) = (C1 + C2t)e^(-4t)`nstants determined by initial conditions.