Final answer:
To find the missing initial condition y''(0) in the given differential equation, we can use the given initial conditions y(0) and y'(0) to solve for it.
Step-by-step explanation:
To find the missing initial condition y''(0) in the given differential equation, we can use the given initial conditions y(0) and y'(0) to solve for it. Differentiating the given equation with respect to x three times, we get:
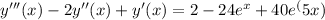
Plugging in x = 0, y(0) = 1/2, and y'(0) = 5/2 into the equation, we can solve for y''(0). Once we find y''(0), we will have the complete initial condition for the problem.