The definite integral representing the area enclosed by the polar curve r = 8, with bounds from
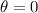 to
to
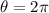 , is
, is
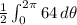 , yielding an area of
, yielding an area of
 .
.
To find the definite integral that represents the area of the region enclosed by the polar curve r = 8, you need to integrate
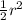 with respect to
with respect to
 over the given bounds. The formula for the area of a polar region is
over the given bounds. The formula for the area of a polar region is
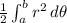 .
.
For the curve r = 8, the definite integral would be:
![\[A = (1)/(2) \int_(0)^(b) (8)^2 \, d\theta\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/i3ceiywaskj1kd90mct0sw9fr4vjmohgtt.png)
You need to determine the upper limit b for the bounds. If you want to find the area of the entire region enclosed by the curve, you need to find where the curve completes one full revolution, which is
 radians. So,
radians. So,
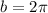 .
.
The definite integral becomes:
![\[A = (1)/(2) \int_(0)^(2\pi) (8)^2 \, d\theta\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/41lp9is7vh06q5kdx68k7u31775s2q1sw0.png)
Simplify and solve this integral to find the area of the region enclosed by the polar curve r = 8.
To complete the expression, we can simplify the integral:
![\[ A = (1)/(2) \int_(0)^(2\pi) 64 \, d\theta \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/z6ae49bza0boloabxpzm5y6lvdls51jq1s.png)
Now, integrate with respect to
 :
:
![\[ A = (1)/(2) \left[ 64\theta \right]_(0)^(2\pi) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yj7g61m01n0uwxwer6dc52af2qa5tvmret.png)
Evaluate the expression at the upper and lower bounds:
![\[ A = (1)/(2) \left[ 64(2\pi) - 64(0) \right] \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/iup48kfbo2xumge63m92llig0xs3q2rus3.png)
Simplify:
![\[ A = (1)/(2) \cdot 128\pi \]\[ A = 64\pi \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/iune0asc19svawta4mjgpepqsxgp4phiwv.png)
So, the definite integral that represents the area of the region enclosed by the polar curve r = 8 with bounds from
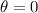 to
to
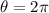 is
is
 .
.