Question

an object of height h is placed at a distance d0 onthe left side of a converging lens of focal length f (f < d0 ).if d0 is chosen so that the image forms at a distance 3.94 fon the right side of the lens, what will be the magnification?(positive result

Answer 1

The object distance d0 must be 1.35f for the image to form at a distance of 4.05f on the right side of the lens. Using this distance, the magnification is found to be -3, indicating an inverted image that is three times larger than the object.

Step-by-step explanation:

To determine the object distance d0 required for an image to form at a distance of 4.05f on the right side of a converging lens, we use the thin-lens equation:

`\((1)/(f) = (1)/(d_0) + (1)/(d_i)\)`

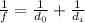
Given d_i (image distance) is 4.05f, the equation becomes:

`\((1)/(f) = (1)/(d_0) + (1)/(4.05f)\)`

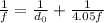
Solving for d0:

`\(d_0 = (4.05f)/(4.05 - 1) = 1.35f\)`

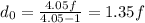
Now, we calculate the magnification m using the formula:

`\(m = -(d_i)/(d_0)\)`

Substituting the known distances:

`\(m = -(4.05f)/(1.35f) = -3\)`

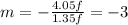
This magnification indicates that the image is inverted and three times larger than the object.




The probable question can be: An object of height h is placed at a distance d0 on the left side of a converging lens of focal length f (f < d0 ).

a) What must d0 be in order for the image to form at a distance 4.05f on the right side of the lens? Give answer as a factor of f.

b) What will be the magnification? (Positive result = upright image, negative result = inverted image).