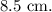The amplitude of the glider's motion, attached to a spring with force constant 180 N/m and initial velocity 0.775 m/s, is approximately 8.5 cm, determined by equating initial kinetic and spring potential energy.
To find the amplitude of the motion using energy conservation, we can equate the initial kinetic energy of the glider to the potential energy stored in the spring at the maximum displacement.
The initial kinetic energy (K.E.) of the glider is given by:
![\[ K.E. = (1)/(2) m v^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/da3d598e56blxhmte1snvapw549z2wm25c.png)
where:
 is the mass of the glider (0.150 kg),
is the mass of the glider (0.150 kg),
 is the initial velocity of the glider (0.775 m/s).
is the initial velocity of the glider (0.775 m/s).
The potential energy (P.E.) stored in the spring at maximum displacement is given by:
![\[ P.E. = (1)/(2) k x^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/u637e4r9l2y6mxg6hrnjsirx119dbz3tj6.png)
where:
\( k \) is the force constant of the spring (180 N/m),
\( x \) is the displacement from the equilibrium position.
At the maximum displacement, all the kinetic energy is converted into potential energy, so we can set
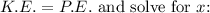
![\[ (1)/(2) m v^2 = (1)/(2) k x^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/fx3l4887upxxhkl4fbycfhhvg1tmhhjcho.png)
Substitute the given values:
![\[ (1)/(2) (0.150 \ \text{kg}) (0.775 \ \text{m/s})^2 = (1)/(2) (180 \ \text{N/m}) x^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/887ywuzct06irqcu471emk9g5t1wdq1o37.png)
Now, solve for \( x \):
![\[ 0.5 * 0.150 * (0.775)^2 = 0.5 * 180 * x^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/iz5mv3akhr1iu2skd0nvjwqb02kbrrnkg4.png)
![\[ 0.05803125 = 90x^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/431nj2aks1jlko7om9ju154r3dv3i4h085.png)
![\[ x^2 = (0.05803125)/(90) \]](https://img.qammunity.org/2024/formulas/physics/high-school/urjz1r4omjc00aljgi5d6cg1yzf6abr2ss.png)
![\[ x = \sqrt{(0.05803125)/(90)} \]](https://img.qammunity.org/2024/formulas/physics/high-school/4vvqiul4ctosr2fyzcpova26jqs70j8wxb.png)
Calculate \( x \) to find the amplitude. Ensure your calculator is set to radians, as the force constant \( k \) is in N/m:
![\[ x \approx 0.085 \ \text{m} \]](https://img.qammunity.org/2024/formulas/physics/high-school/rb9qku3doudchyhhr515mg0h4u9ocze3av.png)
Now, convert the amplitude from meters to centimeters:
![\[ x \approx 8.5 \ \text{cm} \]](https://img.qammunity.org/2024/formulas/physics/high-school/ziyleor5rip38b1j6cp6epj8a1jqvzra65.png)
So, the amplitude of the motion is approximately