Question

Find the long run behavior of each of the following functions. If the function goes to ? or -? enter [infinity] or -[infinity] respectively.

- As x → [infinity], 4(0.5)ˣ→

Answer 1

As the input tends towards certain limits:

-
`\(4(0.5)^x \rightarrow 0\) as \(x \rightarrow \infty\)`

-
`\(7(2.3)^t \rightarrow 0\) as \(t \rightarrow -\infty\)`

-
`\(0.6(2 - 0.3^t) \rightarrow 1.2\) as \(t \rightarrow \infty\)`

`\(4(0.5)^x\) as \(x \rightarrow \infty\):`

As
`\(x\)` tends to positive infinity, the function
`\(4(0.5)^x\)` converges towards 0. Since \(0.5\) raised to increasingly larger positive powers results in smaller positive values, the function approaches zero. Therefore, as
`\(x \rightarrow \infty\),`
`\(4(0.5)^x \rightarrow 0\).`

`\(7(2.3)^t\)`as
`\(t \rightarrow -\infty\)`:

As
`\(t\)` tends to negative infinity, the function
`\(7(2.3)^t\)` approaches zero. This occurs because when the base of an exponential function is greater than 1 (in this case, \(2.3\)), raising it to increasingly negative powers results in smaller positive fractions. Hence, as
`\(t \rightarrow -\infty\), \(7(2.3)^t \rightarrow 0\)`.

.
`\(0.6(2 - 0.3^t)\) as \(t \rightarrow \infty\):`

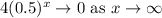
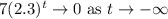
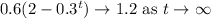
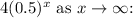
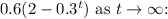
As \(t\) approaches positive infinity, the term \(0.3^t\) where \(0.3\) is raised to larger positive powers, tends toward zero. Therefore, the entire expression
`\(0.6(2 - 0.3^t)\)`approaches
`\(0.6(2 - 0) = 0.6 * 2 = 1.2\) as \(t \rightarrow \infty\).`

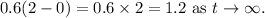
Hence, the long-term behavior for each function is:

-
`\(4(0.5)^x \rightarrow 0\) as \(x \rightarrow \infty\)`

-
`\(7(2.3)^t \rightarrow 0\) as \(t \rightarrow -\infty\)`

-
`\(0.6(2 - 0.3^t) \rightarrow 1.2\) as \(t \rightarrow \infty\)`

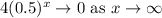
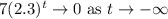
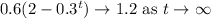
complete the question

Find the long run behavior of each of the following functions. If the function goes to ? or -? enter INFINITY or -INFINITY respectively.

- As x ------> ?, 4(0.5)^(x) ------->

-As t ------> -?, 7(2.3)^(t) -------->

-As t ------> ?, 0.6(2-(0.3)^(t)) ------->