Question

Let the initial value problem be (a) Approximate y(1.1) using Taylor's method of order two with h=0.05. (b) Approximate y(1.1) using Heun's method with h=0.10. You can proceed to approximate the value of y(1.1) using the specified methods and step sizes.

Answer 1

To approximate y(1.1) using Taylor's method of order two with h=0.05, use the formula
`y_n+1 = y_n + h*f(x_n, y_n) + (h^2/2)*f'(x_n, y_n)`

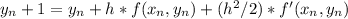
For Heun's method with h=0.10, use the formula
`y_n+1 = y_n + (h/2)*(f(x_n, y_n) + f(x_n+h, y_n+h*f(x_n, y_n))).`

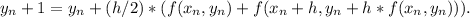
Step-by-step explanation:

To approximate y(1.1) using Taylor's method of order two with h=0.05, we can use the formula:

`y_n+1 = y_n + h*f(x_n, y_n) + (h2/2)*f'(x_n, y_n)`

Where h is the step size and f(x,y) is the derivative of y. Plug in the values for x and y, and calculate the derivative at x=1.1 and y=0.012. Repeat this process to obtain successive approximations. The final value of y(1.1) will be the last approximation we obtained.

To approximate y(1.1) using Heun's method with h=0.10, we can use the formula:

`y_n+1 = y_n + (h/2)*(f(x_n, y_n) + f(x_n+h, y_n+h*f(x_n, y_n)))`

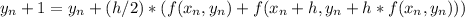
Again, plug in the values for x and y, and calculate the derivative at x=1.1 and y=0.011. Repeat this process to obtain successive approximations. The final value of y(1.1) will be the last approximation we obtained.