Question

The power output of a certain public address speaker is 5.80 W. Suppose it broadcasts equally in all directions.

(a) Within what distance from the speaker would the sound be painful to the ear?

Answer 1

Within a distance of approximately 0.678 meters from the speaker, the sound intensity would be high enough to potentially be painful to the ear.

The loudness or intensity (I) of a sound decreases with the square of the distance from the source, according to the inverse square law. The formula for the intensity of sound is given by:

`\[ I = (P)/(4\pi r^2) \]`

where:

`\( I \)` is the intensity of sound,

`\( P \)` is the power output of the speaker,

`\( r \)` is the distance from the source,

`\( \pi \)` is a constant approximately equal to 3.1416.

In this case, you are given the power output
`(\( P \))` of the speaker, which is 5.80 W. To find the distance
`(\( r \))` at which the sound becomes painful, we can rearrange the formula to solve for
`\( r \)`:

`\[ r = \sqrt{(P)/(4\pi I)} \]`

The painful threshold for sound intensity is subjective, but let's assume it's around
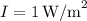`\( I = 1 \, \text{W/m}^2 \)` for this calculation.

`\[ r = \sqrt{(5.80)/(4 \cdot 3.1416 \cdot 1)} \]`

Now, you can plug in the values and calculate
`\( r \)`:

`\[ r = \sqrt{(5.80)/(12.5664)} \]`

`\[ r \approx √(0.4604) \]`

`\[ r \approx 0.678 \, \text{m} \]`

So, within a distance of approximately 0.678 meters from the speaker, the sound intensity would be high enough to potentially be painful to the ear.