Final Answer:
The graph of the function can be sketched as follows:
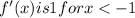 , decreases to 0 at x = 0, stays at 0 until x = 4, and then decreases again. The limit as x approaches 2 of
, decreases to 0 at x = 0, stays at 0 until x = 4, and then decreases again. The limit as x approaches 2 of
 is not determined from the given conditions.
is not determined from the given conditions.
Step-by-step explanation:
To sketch the graph satisfying the given conditions, let's analyze each condition:
1.
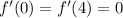 implies that there are critical points at x = 0 and x = 4.
implies that there are critical points at x = 0 and x = 4.
2.
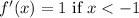 indicates a constant positive slope before x = -1.
indicates a constant positive slope before x = -1.
3.
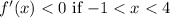 implies a decreasing slope in the interval
implies a decreasing slope in the interval
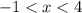
Combining these conditions, we can sketch a function that increases to x = -1, remains constant until x = 0, decreases until x = 4, and remains constant afterward.
However, the limit of
 as
as
 approaches 2 is not specified in the given conditions. It could be any value, and the graph can have various shapes depending on this unspecified limit.
approaches 2 is not specified in the given conditions. It could be any value, and the graph can have various shapes depending on this unspecified limit.