Question

The inverse Laplace transform of X(s)= (s² +25)/10e is given by x(t)=u(t−2)[Acos(5(t−2))+Bsin(5(t−2))] Express A and B as decimal numbers. A= B

Answer 1

The inverse Laplace transform of X(s)= (s² +25)/10e is given by x(t)=u(t−2)[Acos(5(t−2))+Bsin(5(t−2))]. To find A and B, we can use the initial value theorem.

Step-by-step explanation:

The inverse Laplace transform of
`X(s)= (s² +25)/10e`
`X(s)= (s² +25)/10e`

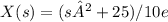
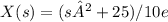
To find A and B, we can use the initial value theorem. This theorem states that if the Laplace transform of a function f(t) is F(s), then the value of f(t) at t=0 is equal to the limit of sF(s) as s approaches infinity.

In this case, the inverse Laplace transform of
`X(s) is x(t)=u(t−2)[Acos(5(t−2))+Bsin(5(t−2))]`titute s=0 into X(s) and equate it to x(0) to solve for A and B.