Question

Find all values of m so that the function y=x m is a solution of the given differential equation. (Enter your answers as a comma-separated list.) x² y² −3xy⁴ +3y=0

Answer 1

To find the values of m so that the function y=x^m is a solution of the given differential equation, we need to substitute the function into the equation and solve for m.

Step-by-step explanation:

To find the values of m for which the function y = x^m is a solution of the given differential equation, we need to substitute the function into the equation and solve for m. The differential equation is
`x^2y^2 - 3xy^4 + 3y = 0`

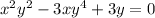
Substituting y = x^m, we get
`x^2(x^m)^2 - 3x(x^m)^4 + 3(x^m) = 0`ain
`x^(2+2m) - 3x^(1+4m) + 3x^m = 0.`

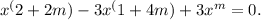
Now, we can equate the coefficients of each power of x to zero and solve for m. For example, equating the coefficient of x^(2+2m) to zero gives us 2+2m = 0. Solving this equation, we find m = -1. Repeat this process for the other coefficients to find the values of m.