Question

In a certain reference frame, a particle with momentum of 7 mev/c and a total energy of 9 mev.

(a) determine the mass of the particle. _______ mev/c²

Answer 1

The rest mass of the particle is determined using the relativistic energy-momentum relation. Substituting given values into the equation yields the rest mass, expressed in MeV/c².

To determine the mass of the particle, we can use the relativistic energy-momentum relation, which relates the energy (E), momentum (p), and mass (m) of a particle. The equation is given by:

`\[ E^2 = (pc)^2 + (m_0c^2)^2 \]`

where:

- (E) is the total energy of the particle,

- (p) is the momentum of the particle,

-
`\(m_0\)` is the rest mass of the particle,

- (c) is the speed of light in a vacuum.

Given that the momentum (p) is 7 MeV/c and the total energy (E) is 9 MeV, we can substitute these values into the equation:

`\[ (9 \, \text{MeV})^2 = (7 \, \text{MeV/c})^2 + (m_0c^2)^2 \]`

Solving for
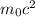`\(m_0c^2\)`, the rest mass-energy of the particle, gives:

`\[ (m_0c^2)^2 = (9 \, \text{MeV})^2 - (7 \, \text{MeV/c})^2 \]`

Finally, taking the square root of
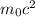`\(m_0c^2\)` gives the rest mass of the particle:

`\[ m_0c^2 = \sqrt{(9 \, \text{MeV})^2 - (7 \, \text{MeV/c})^2} \]`

Now, the obtained value represents the rest mass-energy
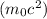`(\(m_0c^2\))` of the particle in units of MeV/c². To find the rest mass
`(\(m_0\))`, this value needs to be divided by
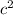`\(c^2\)`, the square of the speed of light.