Alice's solution x is proven equal to Bob's plaintext m using the Chinese remainder theorem and Euler's theorem. Both x and m are congruent modulo N, ensuring successful decryption.
To prove that Alice's solution x is equal to Bob's plaintext m, we need to show that:
![\[ x \equiv m \pmod{N} \]](https://img.qammunity.org/2024/formulas/computers-and-technology/high-school/20ono8pxfhkuqrv9y1hh8985ny3o9q28ny.png)
Here's the proof:
1. Alice uses the Chinese remainder theorem to solve the pair of congruences:
![\[ x_1 \equiv C_1^((p-1)) \pmod{p} \] \[ x_2 \equiv C_2^((q-1)) \pmod{q} \]](https://img.qammunity.org/2024/formulas/computers-and-technology/high-school/psoj43lkt0kifnky84a61a58yvo58a24jc.png)
2. According to the Chinese remainder theorem, there exists a unique solution x modulo N that satisfies the following conditions:
![\[ x \equiv x_1 \pmod{p} \] \[ x \equiv x_2 \pmod{q} \]](https://img.qammunity.org/2024/formulas/computers-and-technology/high-school/uk3vrt7k5ke5rjoj6rlvrgelksjupfn3y3.png)
3. Substituting the values of
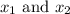 :
:
![\[ x \equiv C_1^((p-1)) \pmod{p} \] \[ x \equiv C_2^((q-1)) \pmod{q} \]](https://img.qammunity.org/2024/formulas/computers-and-technology/high-school/5c5dsdoj7erylk8sf90inpxkxv0cl7tnav.png)
4. By Euler's theorem,
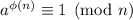 where
where
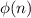 is Euler's totient function.
is Euler's totient function.
Applying Euler's theorem:
![\[ C_1^((p-1)) \equiv 1 \pmod{p} \] \[ C_2^((q-1)) \equiv 1 \pmod{q} \]](https://img.qammunity.org/2024/formulas/computers-and-technology/high-school/2wnefkc56vonnb21ml2p2zengts6rtxr9q.png)
5. Substituting back into the Chinese remainder theorem equations:
![\[ x \equiv 1 \pmod{p} \] \[ x \equiv 1 \pmod{q} \]](https://img.qammunity.org/2024/formulas/computers-and-technology/high-school/5g3jh2cw95s958hbh68pv90gxha92fhndg.png)
6. Combining the congruences using the Chinese remainder theorem, we get:
![\[ x \equiv 1 \pmod{p}q = N \]](https://img.qammunity.org/2024/formulas/computers-and-technology/high-school/45htdy8fqpqggw707wttedy74c1bhgge96.png)
7. Thus,
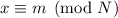 , and we have proved that Alice's solution x is equal to Bob's plaintext m.
, and we have proved that Alice's solution x is equal to Bob's plaintext m.