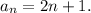The generating function for the recurrence relation
 with
with
 is
is
 . The solution to the recurrence relation is
. The solution to the recurrence relation is
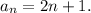
To find the generating function for the given recurrence relation
 with
with
 , let's define the generating function \(A(x)\) as:
, let's define the generating function \(A(x)\) as:
![\[ A(x) = \sum_(n=0)^(\infty) a_n x^n \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/gm285j9zjrbuw3hapac7z5et1rdn66b94m.png)
Now, we can express the given recurrence relation in terms of the generating function:
![\[ A(x) = a_0 + a_1x + a_2x^2 + \dots \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yfz0zwtteqin2kfjfhraimw5bg1eyttu0a.png)
![\[ A(x) = 1 + (a_0 + 2)x + (a_1 + 2)x^2 + \dots \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/13iq7wzrv5ml2dspqpyutbvokai4nuuubi.png)
Now, noticing that
 , we can express the generating function as:
, we can express the generating function as:
A(x) = 1 + (A(x) + 2)x
Solving for A(x):
![\[ A(x) = (1)/(1-x) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/me0qky1ak56320n43459udix44a9qb16ru.png)
Now, to solve the recurrence relation, we can expand A(x) into a power series:
![\[ A(x) = 1 + x + x^2 + x^3 + \dots \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/twk08vvsscpzhwwz1eeigs3vmdxsb25doi.png)
Thus, the solution to the recurrence relation
 with
with
 is
is