The angular dispersion of a 600 lines per mm amplitude grating at 400 nm is 45 degrees.
To compute the angular dispersion of a 600 lines per mm amplitude grating at 400 nm, we can use the following formula:
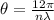
where
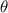 is the angular dispersion,
is the angular dispersion,
 is the grating constant (600 lines/mm), and
is the grating constant (600 lines/mm), and
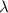 is the wavelength of light (400 nm). Plugging in the values, we get:
is the wavelength of light (400 nm). Plugging in the values, we get:
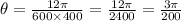
Thus, the angular dispersion for a 600 lines per mm amplitude grating at 400 nm is:
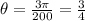
In degrees, this is:
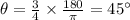
So, the angular dispersion of a 600 lines per mm amplitude grating at 400 nm is 45 degrees.